sclubnax.blogg.se

These distances will be at a minimum at the centroid and will get larger as we start further from the centroid. The distances used in our moment integrals depends on the point or axis chosen. Specifically, the further we move from the centroid, the larger the average distances become. If we pick a different point or axis to take the moment of inertia about, then on average all the distances in our moment integral will be a little bit bigger. Because the centroid of a shape is the geometric center of an area or volume, the average distance to any one point in a body is at a minimum.

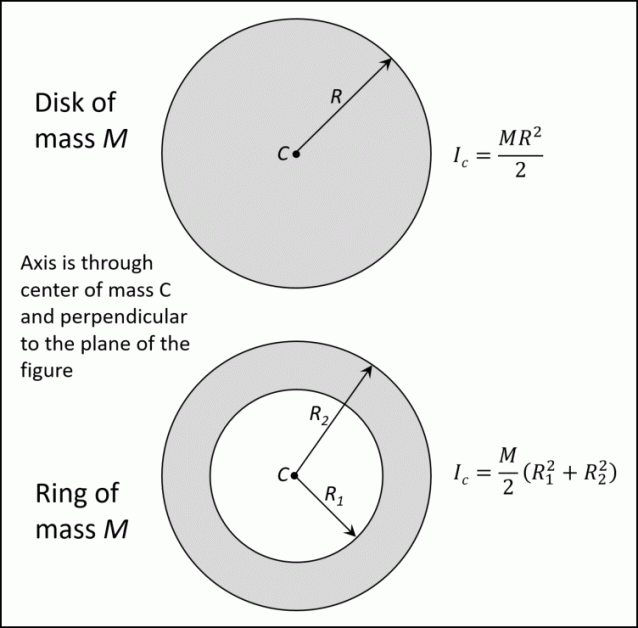
We then measured all distances from that point or axis, where the distances were the moment arms in our moment integrals. When we calculated the area and mass moments of inertia via integration, one of the first things we had to do was to select a point or axis we were going to take the moment of inertia about. Once the moments of inertia are adjusted with the Parallel Axis Theorem, then we can add them together using the method of composite parts. We will use something called the Parallel Axis Theorem to adjust the moments of inertia so that they are all taken about some standard axis or point. Because each part has its own individual centroid coordinate, we cannot simply add these numbers. The moments of inertia in the table are generally listed relative to that shape's centroid though. Moments of inertia for the parts of the body can only be added when they are taken about the same axis. As discussed on the previous pages, the area and mass moments of inertia are dependent upon the chosen axis of rotation.

This method is known as the method of composite parts.Ī key part to this process that was not present in centroid calculations is the adjustment for position. In this method we will break down a complex shape into simple parts, look up the moments of inertia for these parts in a table, adjust the moments of inertia for position, and finally add the adjusted values together to find the overall moment of inertia. Method of Composite Parts for Moments of Inertia and the Parallel Axis TheoremĪs an alternative to integration, both area and mass moments of inertia can be calculated via the method of composite parts, similar to what we did with centroids.